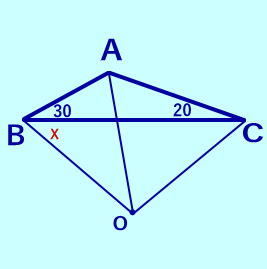
三角形 の 外 心 - 欧拉公式（有关三角形的内外心距离）_外接圆
三角形の五心
三角形の五心
三角形の重心
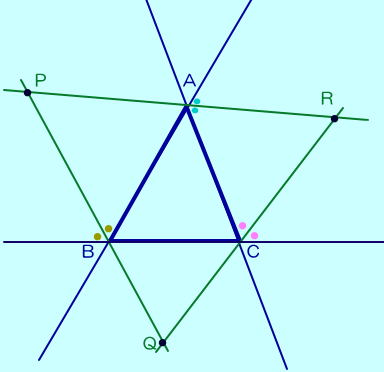
三角形の五心（内心,外心,重心,垂心,傍心）の性質と証明を解説！
傍心は内心との類似点が多いので、行き詰ったときは内心の考え方でも試してみましょう。
证明 ： （1）连接AI，并延长，与外接圆相交于点E。
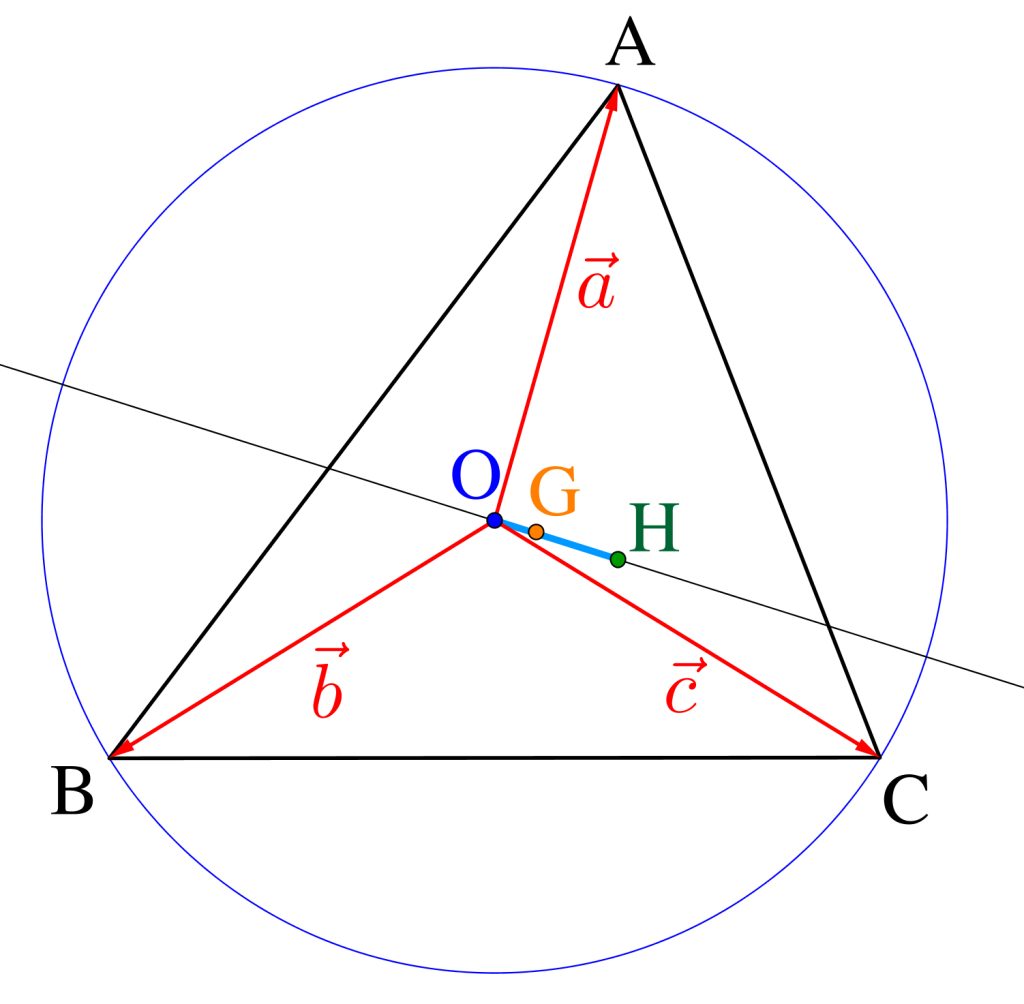
欧拉公式（有关三角形的内外心距离）_外接圆
詳しい証明が知りたい方は「」をご覧ください。
共点であることを示すためにがよく利用される。
三角形
再把连接内、外心的线段OI向两端延长，与外接圆分别相交于点G和H。
また二等辺三角形には、定義から導き出される性質（定理）があります。
欧拉公式（有关三角形的内外心距离）_外接圆
二等辺三角形の特徴は2つあります。
歴史 [ ] 内心・外心・重心・垂心・傍心などは古くから知られており、の「」にも記述が見られる。
三角形の五心（内心,外心,重心,垂心,傍心）の性質と証明を解説！
数学で重要な図形なので、定義や性質、合同条件を覚えたうえで問題を解きましょう。
- の中心。
三角形の傍心とは？傍心の性質と証明を解説！
角度が等しいだけでは絶対に合同とはいえません。
また、ある三角形 Aにおいて、辺の長さの比が、 p : q : r であり、別の三角形 Bにおいて、辺の長さの比も、 p : q : r である場合には、三角形 Aの辺の長さが ap, aq, ar とおけて、三角形 Bの辺の長さが bp, bq, br とおける。
三角形の中心
ここで r はの半径である。
一般的な三角形には斜辺がありません。
- 関連記事
2021 www.dfe.millenium.inf.br