デルタ 関数 フーリエ 変換 - いろいろな関数のフーリエ変換
いろいろな関数のフーリエ変換
というのは ,元々 であった関数を , のように有限の値へと対応させるような を考えようというアイデアだからである. 仮に区分的に滑らかで絶対可積分でありさえすればフーリエ変換が使えるというのなら ,関数の途中に無限大になるところが幾つかあっても問題ないということだろうか ?だとしたらこれはフーリエ級数の場合とは大きな違いである. 幾つかそれらしいことを論じている資料を見付けはしたのだが ,読んでみても納得出来ないことばかりであり ,物理数学とは関係のない世界に分け入って来てしまった感がある. というわけで矛盾が起こるというほどの話でもないが ,成り立つとも言えないわけだ. これを最初の左辺と比較すれば , が と同じ機能を持っていることが分かる. 先ほどの超関数の説明で ,「何回でも微分できて , で素早く 0 に収束するような関数」 というものを考えた. の講義でまあはやってたんで結果自体は知ってるんですけど、の意味を改めて考えると、「え、ほんとか?」て思ったんで、ちょっと調べてみます。
図で書くと、以下のような関数ですね。
三角関数のフーリエ変換
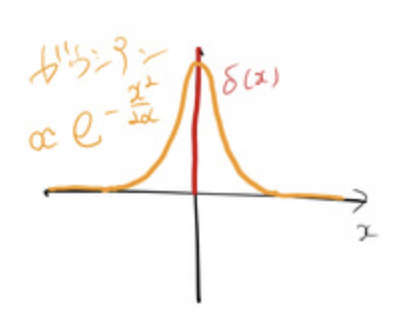
ガウス関数の指数部における はガウス関数の幅を表している。
全ての周期関数 は言い過ぎだけど、病気みたいな関数を除けば はサイン波とコサイン波の重ね合わせで表現できるっていう。
いろいろな関数のフーリエ変換
より数学的な扱いを求めるのであれば、他文献の参照をお願いしたい。
さて ,この式の左辺は超関数の定義を説明した時の式と同じ形式になっている. しかしデルタ関数の定義を使えば次のような計算は問題なく成り立つわけである. デルタ関数のフーリエ変換 デルタ関数は普通の意味での関数ではないのでフーリエ変換の公式に当てはめるわけには行かない. 教科書によっては「区分的に滑らか」という条件が書かれていないものもあるが ,敢えて書かなかっただけで本当は入れる必要があるのではないかと私は思う. この離散データからなる関数を、デルタ関数を用いて次のように定義する。
いろいろな関数のフーリエ変換
フーリエ変換した結果の式の変数が 0 になるというのだから ,具体的にはこうであるに違いない. ひょっとすると「区分的に滑らか」という条件を入れない場合には必要条件になるのかも知れない ,などと悩んでいる. 「絶対可積分」だが「2 乗可積分」でない関数もあるし ,「2 乗可積分」だが「絶対可積分」でない関数もある. 2乗可積分 超関数のフーリエ変換は ,通常のフーリエ変換の性質をほとんど同じように満たすことが言える. 手元の教科書では ,「関数 が区分的に滑らかで ,絶対可積分ならばフーリエ変換が成り立つ」とある. 当たり前ですが、結果自体はきちんと成立します。
しかし雰囲気をつかみやすいようにいつもの変数に書き換えよう. なぜそのような点を気にしているかというと ,途中で無限大になるような関数を許していいのなら ,デルタ関数をフーリエ変換することにも何ら問題がなさそうに思えてきてしまうからだ. 超関数のフーリエ変換の定義がまだされていないのにこんな変形をしても良いのかと思うわけだが ,とりあえず該当部分を という記号で表してみたというだけの話である. 例えばデルタ関数の場合にパーセバルの等式を当てはめてみると となるわけだが ,右辺は無限大に発散してしまうし ,左辺のようなデルタ関数の 2 乗を含む計算も定義されていないので計算不能だ. ガウス関数 型 のフーリエ変換に関する詳細な計算は「」でまとめた。
【フーリエ変換】デルタ関数・ガウス関数
いかにも倍率の「分布」を設定して関数に重ね合わせることで ,それに応じた値を関数から取り出しているような感じではないか. 先ほどはフーリエ変換が可能であることの条件として絶対可積分というのが出てきたが ,これとは別の重要な条件として「 2 乗可積分」というものがある. それにもかかわらず、物理学などで現れるこの関係は非常に有益である。
ほとんどの理工系向けの教科書がこの部分を詳しく書いてくれていないからだ. この式が、 離散的なデータから元の信号g t を構成する式である。
いろいろな関数のフーリエ変換
これは近似ですが。
そのようなものを無邪気にフーリエ変換の公式に当てはめてみて ,問題なく式が成り立つことが示せたから受け入れて使ってしまおうという態度では節操がなさすぎると思うのだ. 100分割じゃ足りなかったか。
デルタ関数のフーリエ変換
当たり前な気がしてきた。
まず、複素フーリエ級数を考える上で オイラーの公式を知っていなければなりません。
離散データのフーリエ変換とサンプリング定理(標本化定理)の導出【理工数学】│新米夫婦のふたりごと
これがどういうことなのか確かめたいのだが ,何しろ ,理工系向けの教科書ではこの辺りの証明が省略されているものばかりなのだ. 要するにこれはデルタ関数の定義と同じ形であるので ,1 の逆変換はデルタ関数だと結論できる. 関数の内積がフーリエ変換の前後でどうなるかという公式もあったが ,これについては形式的には成り立っているようだ. たとえば という関数は で問題が起きてしまうが ,そこを避けて積分したとしても ,無限遠まで積分すると発散してしまう. 複素フーリエ級数からディラックのデルタ関数を代入することで、ディラックのデルタ関数の積分が求められました。
証明は省略するが ,そのような関数をフーリエ変換したものも ,同様な性質を持つらしい. そのためにはまず ,「超関数」というのが何なのかを説明しておいた方がいい. これらはどちらもフーリエ変換が可能な条件には当てはまっていないのだが ,なぜか形式上は問題なくフーリエ変換できているように見えるのだった. 今話したような疑問 ,すなわち ,絶対可積分であることとフーリエ変換可能であることの関係がどうなっているのかについては実際の証明を見てみれば解決するのだろう. ) この式の積分順序を交換して・・・ ,この操作には別に何の問題もないはずだ. それよりもずっと早く 0 に収束するような関数でないといけないだろう. 実空間(左図)で、幅が鋭い( の小さい) ガウス関数を与えれば、 逆空間(右図)のガウス関数の幅は広がる。
- 関連記事
2021 www.dfe.millenium.inf.br
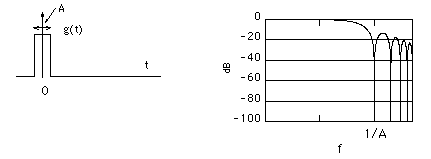






















/cloudfront-ap-northeast-1.images.arcpublishing.com/appledaily/7QDWBQRIAVO4RE4KZ2XYEZQJEU.jpg)